viccch.github.io
Delaunay三角剖分与TIN的构建
Introduction
Delaunay三角剖分
三角剖分triangulation就是对给定的平面点集P,生成三角形集合T的过程,得到的所有三角形顶点恰好构成集合P,任意两个三角形的边不相交,所有三角形的合集构成P的凸包(convex hull)。
一般来说给定一个点集,往往存在不止一个三角剖分。
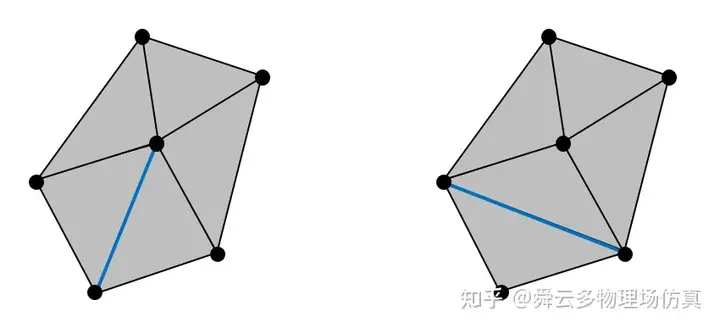
由于给定点集的三角剖分不唯一,我们希望从中挑选出一个“最优”的三角剖分。那么何为最优呢?这涉及到对三角形“质量”(quality)的评定。一般在数值计算中,我们不希望三角形过于狭长,也就是说越接近等边三角形越好。以下是几种常见的质量评定标准:
a) 最小角(minimum angle):即所有三角形的内角当中最小的角。
b) 纵横比(aspect ratio):三角形最短边与最长边的比例。
c) 半径比(radius ratio):三角形内接圆半径的两倍与外接圆半径的比例。
Delaunay三角剖分
所有三角形的外接圆均满足空圆性质的三角剖分,称为一个Delaunay三角剖分。
空圆性质
即一个三角形(或边)的外接圆范围内(边界除外),不包含点集P中的任何顶点。
对于上面的例子来说,左图的三角剖分是Delaunay的,任何一个三角形的外接圆内部都不包含点集中的顶点;而右图的三角剖分不是Delaunay的,因为下面的两个三角形的外接圆内部都包含了顶点。
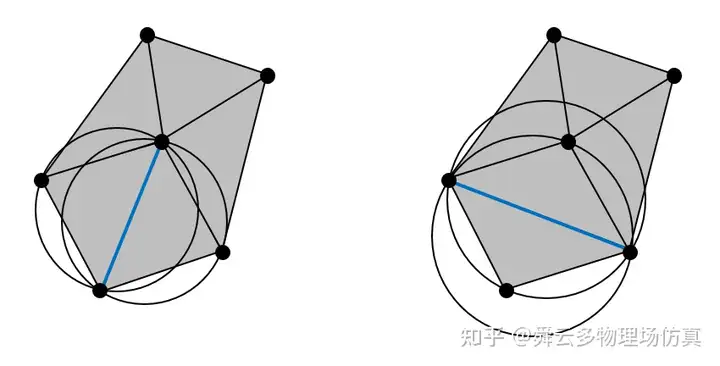
参考:https://zhuanlan.zhihu.com/p/459884570
TIN
不规则三角网(Triangulated Irregular Network,TIN)是一种表示数字高程模型的方法。它减少了规则格网带来的数据冗余,同时在吉萨un效率方面优于纯粹基于等高线的方法。
在TIN中,满足最佳三角形的条件为:尽可能的保证三角形的三个角都是锐角,三角形的三条边近似相等,最小角最大化。
TIN 是基于矢量的数字地理数据的一种形式,通过将一系列折点(点)组成三角形来构建。形成这些三角形的插值方法有很多种,例如 Delaunay 三角测量法或距离排序法。ArcGIS 支持 Delaunay 三角测量方法。
TIN 的单位是英尺或米等长度单位,而不是度分秒。当使用地理坐标系的角度坐标进行构建时,Delaunay 三角测量无效。创建 TIN 时,应使用投影坐标系(PCS)。
TIN 模型的适用范围不及栅格表面模型那么广泛,且构建和处理所需的开销更大。获得优良源数据的成本可能会很高,并且,由于数据结构非常复杂,处理 TIN 的效率要比处理栅格数据低。
TIN 通常用于较小区域的高精度建模(如在工程应用中),此时 TIN 非常有用,因为它们允许计算平面面积、表面积和体积。