lectures
第6次作业
1.填空题
间接平差法误差方程的形式为____
\[V=B\hat{x}-l\]2.
间接平差中误差方程的个数和平差参数的个数分别为__和__
n,t
3.计算
设有等精度观测的条件方程为$\begin{aligned}v_1-v_2+v_3+2=0\v_3+v_4+v_7+1=0\v_2+v_5+v_6+v_7-1=0\end{aligned}$,试组成法方程。
\[\begin{bmatrix} 1&-1&1&0&0&0&0\\ 0&0&1&1&0&0&1\\ 0&1&0&0&1&1&1\\ \end{bmatrix} \begin{bmatrix} v_1\\v_2\\v_3\\v_4\\v_5\\v_6\\v_7\\ \end{bmatrix} +\begin{bmatrix} 2\\1\\-1 \end{bmatrix}=0\]等权观测,则 \(N_{aa}=AP^{-1}A^T =\begin{bmatrix} 1&-1&1&0&0&0&0\\ 0&0&1&1&0&0&1\\ 0&1&0&0&1&1&1\\ \end{bmatrix} \begin{bmatrix} 1&&&&&&\\ &1&&&&&\\ &&1&&&&\\ &&&1&&&\\ &&&&1&&\\ &&&&&1&\\ &&&&&&1\\ \end{bmatrix} \begin{bmatrix} 1&0&0\\ -1&0&1\\ 1&1&0\\ 0&1&0\\ 0&0&1\\ 0&0&1\\ 0&1&1\\ \end{bmatrix} =\begin{bmatrix} 3&1&-1\\ 1&3&1\\ -1&1&4\\ \end{bmatrix}\)
法方程为:$NK-W=0$,即 \(\begin{bmatrix} 3&1&-1\\ 1&3&1\\ -1&1&4\\ \end{bmatrix} \begin{bmatrix} k_a\\k_b\\k_c \end{bmatrix} +\begin{bmatrix} 2\\1\\-1 \end{bmatrix}=0\)
4.
在图所示的水准网中,A、B点位已知水准点,C、D点为待定的水准点,已知$H_A=15.000m、H_B=18.303m$,同精度独立观测的高差观测值为:$h=(1.258m,2.041m,1.571m,1.724m)^T$。试按条件平差求(1)各段高差平差值及其中误差;(2)C、D点高程平差值及其中误差。
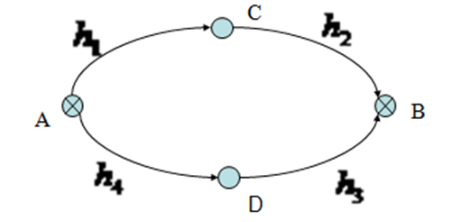
条件方程: \(\hat{h_1}+\hat{h_2}=H_B-H_A\\ \hat{h_3}+\hat{h_4}=H_B-H_A\\\)
$\hat{h_1}=h_i+v_i$ 代入改正数方程(mm): \(v_1+v_2-4=0\\ v_3+v_4-8=0\\\)
即 \(\begin{bmatrix} 1&1&0&0\\ 0&0&1&1\\ \end{bmatrix} \begin{bmatrix} v_1\\v_2\\v_3\\v_4 \end{bmatrix} +\begin{bmatrix} -4\\-8 \end{bmatrix} =0\)
系数阵: \(N=AP^{-1}A^T =\begin{bmatrix} 1&1&0&0\\ 0&0&1&1\\ \end{bmatrix} \begin{bmatrix} 1&&&\\ &1&&\\ &&1&\\ &&&1\\ \end{bmatrix} \begin{bmatrix} 1&0\\1&0\\0&1\\0&1\\ \end{bmatrix} =\begin{bmatrix} 2&0\\0&2\\ \end{bmatrix}\)
法方程:$NK-W=0$即 \(\begin{bmatrix} 2&0\\0&2\\ \end{bmatrix}\begin{bmatrix} k_a\\k_b\\ \end{bmatrix} +\begin{bmatrix} -4\\-8 \end{bmatrix} =0\)
得 \(K=\begin{bmatrix} 2\\4 \end{bmatrix}\)
由$v=QA^TK$ \(v=\begin{bmatrix} 1&&&\\ &1&&\\ &&1&\\ &&&1\\ \end{bmatrix} \begin{bmatrix} 1&0\\1&0\\0&1\\0&1\\ \end{bmatrix} \begin{bmatrix} 2\\4 \end{bmatrix} =\begin{bmatrix} 2\\2\\4\\4 \end{bmatrix}\)
则 (1)$h_1,h_2,h_3,h_4$各段高差平差中误差分别为$\begin{bmatrix}2&2&4&4\end{bmatrix}^T$mm,高差平差值为$\begin{bmatrix}1.260&2.043&1.575&1.728\end{bmatrix}^T$m
(2)C中误差为$2$mm,平差值为16.260m,D中误差为$4$mm,平差值为16.728m
5.
已知间接平差的函数模型为:$\left.\begin{aligned} &V=B\hat{x}-l\&l=L-(BX^0+d) \end{aligned}\right }$,试根据最小二乘原理$V_TPV=min$,导出间接平差的基础方程、法方程和解的形式。
\(L+V=B\hat{X}+d\) 令 \(\hat{X}=X^0+\hat{x}\) \(l=L-(BX^0+d)\) \(V=B\hat{x}-l\) \(\frac{\partial{V^TPV}}{\partial{\hat{x}}}=2V^TP\frac{\partial{V}}{\partial{\hat{x}}}=V^TPB=0\) \(B^TPV=0\) \(B^TPB\hat{x}-B^TPl=0\) 令$N_{bb}=B^TPB$,$W=B^TPl$ 则法方程 \(N_{bb}\hat{x}-V=0\\\hat{x}=N_{bb}^{-1}W\) \(\hat{L}=L+V\qquad\hat{X}=X^0+\hat{x}\)
6.
在图所示的水准网中,A、B、C为已知水准点,高差观测值及路西那长度如下:$h_1=+1.003m$,$h_2=+0.501m$,$h_3=+0.503m$,$h_4=+0.505m$;$S_1=1km$,$S_2=2km$,$S_3=2km$,$S_4=1km$。已知$H_A=11.000m$,$H_B=11.500m$,$H_C=12.008m$,试用间接平差法求$P_1$及$P_2$点的高程平差值。
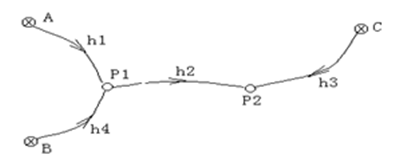
(1)选参数
设P1,P2高程分别是$X_1,X_2$
(2)列误差方程 \(\hat{h_1}=\hat{X_1}-H_A\\ \hat{h_2}=\hat{X_2}-\hat{X_1}\\ \hat{h_3}=\hat{X_2}-H_C\\ \hat{h_4}=\hat{X_1}-H_B\\\)
代入$\hat{h_i}=v_i+h_i$误差方程,得: \(v_1=\hat{X_1}+12.003\\ v_2=\hat{X_2}-\hat{X_1}-0.501\\ v_3=\hat{X_2}-12.511\\ v_4=\hat{X_1}-12.005\\\)
即 \(\begin{bmatrix} v_1\\v_2\\v_3\\v_4 \end{bmatrix} =\begin{bmatrix} 1&0\\-1&1\\0&1\\1&0 \end{bmatrix} \begin{bmatrix} \hat{X_1}\\\hat{X_2} \end{bmatrix} +\begin{bmatrix} 12.003\\-0.501\\-12.511\\-12.005 \end{bmatrix}\)
\[X_0=\begin{bmatrix} X^0_1\\X^0_2\\ \end{bmatrix} =\begin{bmatrix} 12.003\\12.511 \end{bmatrix}\] \[\begin{bmatrix} v_1\\v_2\\v_3\\v_4 \end{bmatrix} =\begin{bmatrix} 1&0\\-1&1\\0&1\\1&0 \end{bmatrix} \begin{bmatrix} \delta\hat{X_1}\\\delta\hat{X_2} \end{bmatrix} -\begin{bmatrix} 0\\-7\\0\\2 \end{bmatrix}\] \[P=\begin{bmatrix} 1&&&\\&\frac{1}{2}&&\\&&\frac{1}{2}&\\&&&1\\ \end{bmatrix}\] \[N=B^TPB= \begin{bmatrix} 1&-1&0&1\\0&1&1&0 \end{bmatrix} \begin{bmatrix} 1&&&\\&\frac{1}{2}&&\\&&\frac{1}{2}&\\&&&1\\ \end{bmatrix} \begin{bmatrix} 1&0\\-1&1\\0&1\\1&0 \end{bmatrix} =\begin{bmatrix} 2.5&-0.5\\ -0.5&1\\ \end{bmatrix}\] \[W=B^TPl=\begin{bmatrix} 1&-1&0&1\\0&1&1&0 \end{bmatrix} \begin{bmatrix} 1&&&\\&\frac{1}{2}&&\\&&\frac{1}{2}&\\&&&1\\ \end{bmatrix} \begin{bmatrix} 0\\-7\\0\\2 \end{bmatrix} =\begin{bmatrix} 5.5\\-3.5 \end{bmatrix}\](3)组成法方程: $N\hat{x}-W=0$
\[\begin{bmatrix} 2.5&-0.5\\ -0.5&1\\ \end{bmatrix} \begin{bmatrix} \delta\hat{X_1}\\\delta\hat{X_2} \end{bmatrix} -\begin{bmatrix} 5.5\\-3.5 \end{bmatrix} =0\](4)法方程解算:$\hat{x}=N^{-1}W$ \(\begin{bmatrix} \delta\hat{X_1}\\\delta\hat{X_2} \end{bmatrix} =\begin{bmatrix} 2.5&-0.5\\ -0.5&1\\ \end{bmatrix}^{-1} \begin{bmatrix} 5.5\\-3.5 \end{bmatrix} =\begin{bmatrix} \frac{5}{3}\\-\frac{8}{3} \end{bmatrix}\)
$\hat{L}=L+V,\hat{X}=X^0+\hat{x}$:
\[\hat{X}=\begin{bmatrix} X^0_1\\X^0_2\\ \end{bmatrix} +\begin{bmatrix} \delta\hat{X_1}\\\delta\hat{X_2} \end{bmatrix} =\begin{bmatrix} 12.0047\\12.5083 \end{bmatrix}\]