lectures
第5次作业
1.简答
条件平差中求解的未知量是什么?能否由$AV-W=0$直接求出?
未知量是改正数。
不能直接求出,因为结果不唯一。
条件平差的前提是有多余观测量,条件方程式的个数与多余观测量有关,每有一个多余观测量,就可列出一个独立的条件方程式,在进行条件平差时,应列出与多余观测数相同的独立的条件方程式。
2.计算
在图中同精度独立观测了测站A附近的角度,得观测值为:$L_1=60^\circ00^\prime00^{\prime\prime}、L_2=60^\circ00^\prime00^{\prime\prime}、L_3=240^\circ00^\prime25^{\prime\prime}、L_4=120^\circ00^\prime05^{\prime\prime}$,试用条件平差法求各角平差值。
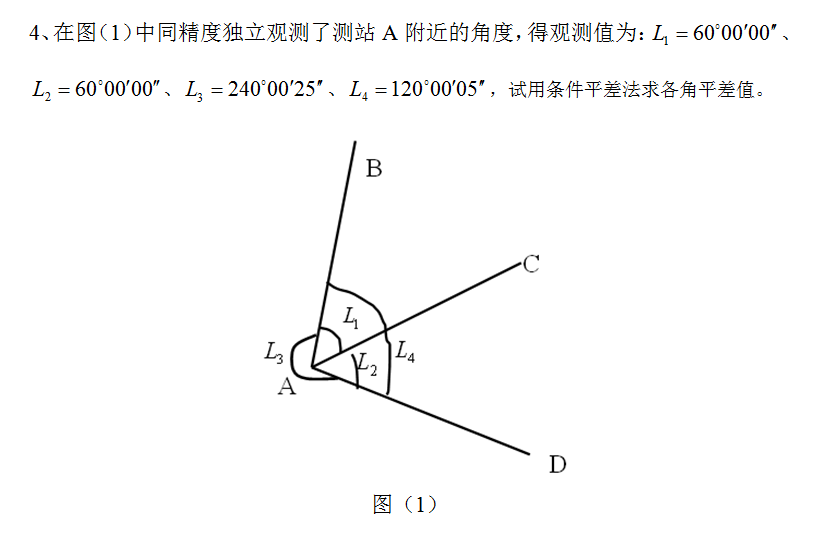
- ans: n=4,t=2,r=n-t=2
条件方程: \(\hat{L_1}+\hat{L_2}-\hat{L_4}=0\\ \hat{L_3}+\hat{L_4}-360^\circ=0\)
将$\hat{L_i}=L_i+v_i$带入得改正数方程: \(v_1+v_2-v_4-5^{\prime\prime}=0\\ v_3+v_4+30^{\prime\prime}=0\)
即 \(\begin{bmatrix}1&1&0&-1\\0&0&1&1\end{bmatrix}\begin{bmatrix}v_1\\v_2\\v_3\\v_4\end{bmatrix}+\begin{bmatrix}-5\\30\end{bmatrix}=0\)
设各角权相等, 系数阵 \(N_{aa}=AP^{-1}A^T=\begin{bmatrix}1&1&0&-1\\0&0&1&1\end{bmatrix}\begin{bmatrix}1&&&\\&1&&\\&&1&\\&&&1\end{bmatrix}\begin{bmatrix}1&0\\1&0\\0&1\\-1&1\end{bmatrix}=\begin{bmatrix}3&-1\\-1&2\end{bmatrix}\)
法方程为 $\begin{bmatrix}3&-1\-1&2\end{bmatrix}\begin{bmatrix}k_1\k_2\end{bmatrix}+\begin{bmatrix}-5\30\end{bmatrix}=0$
即 \(\left. \begin{aligned} 3k_a-k_b-5=0\\ -k_a+2k_b+30=0 \end{aligned} \right \}\)
则 $K=-N_{aa}^{-1}W$,解得$\left { \begin{aligned}k_a=-4\k_b=-17\end{aligned}\right.$
改正数 \(v=QA^TK=\begin{bmatrix}1&&&\\&1&&\\&&1&\\&&&1\end{bmatrix}\begin{bmatrix}1&0\\1&0\\0&1\\-1&1\end{bmatrix}\begin{bmatrix}-4\\-17\end{bmatrix}=\begin{bmatrix}-4\\-4\\-17\\-13\end{bmatrix}\)
检验: \(\hat{L_1}+\hat{L_2}-\hat{L_4}=0\\ \hat{L_3}+\hat{L_4}-360^\circ=0\)
3.
在下图中,同精度独立观测了个高差,得观测值为:$h_1=1.576m,h_2=2.215m,h_3=-3.800m,h_4=0.871m,h_5=-2.438m,h_6=-1.350m$。试用条件平差求个高差平差值。
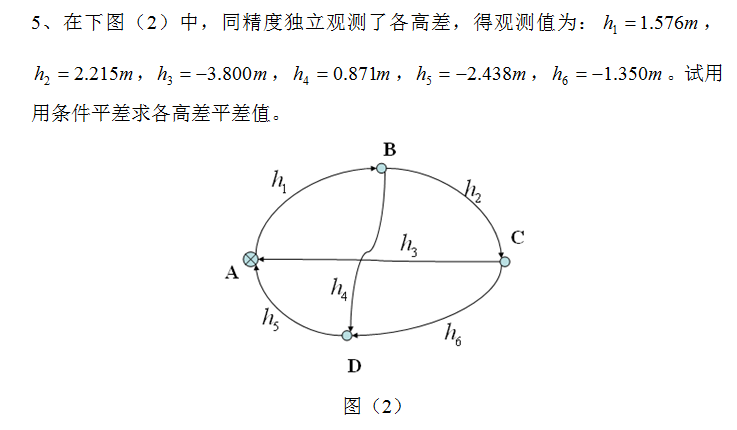
- ans: n=6,t=3,r=n-t=3
条件方程: \(\hat{h_3}=\hat{h_5}+\hat{h_6}\\ \hat{h_3}=-\hat{h_1}-\hat{h_2}\\ \hat{h_4}=\hat{h_2}+\hat{h-6}\)
将$\hat{h_i}=h_i+v_i$带入得改正数方程(mm): \(v_3-v_5-v_6-12=0\\ v_3+v_1+v_2-9=0\\ v_4-v_2-v_6+6=0\)
即 \(\begin{bmatrix}0&0&1&0&-1&-1\\1&1&1&0&0&0\\0&-1&0&1&0&-1\end{bmatrix}\begin{bmatrix}v_1\\v_2\\v_3\\v_4\\v_5\\v_6\end{bmatrix}+\begin{bmatrix}-12\\-9\\6\end{bmatrix}=0\)
设各边权相等, 系数阵 \(N_{aa}=AP^{-1}A^T=\begin{bmatrix}0&0&1&0&-1&-1\\1&1&1&0&0&0\\0&-1&0&1&0&-1\end{bmatrix}\begin{bmatrix}1&&&&&\\&1&&&&\\&&1&&&\\&&&1&&\\&&&&1&\\&&&&&1\end{bmatrix}\begin{bmatrix}0&1&0\\0&1&-1\\1&1&0\\0&0&1\\-1&0&0\\-1&0&-1\end{bmatrix}=\begin{bmatrix}3&1&1\\1&3&-1\\1&-1&3\end{bmatrix}\)
法方程为
\(\begin{bmatrix}3&1&1\\1&3&-1\\1&-1&3\end{bmatrix}\begin{bmatrix}k_a\\k_b\\k_c\end{bmatrix}+\begin{bmatrix}-12\\-9\\6\end{bmatrix}=0\)
解得$\begin{bmatrix}k_a\k_b\k_c\end{bmatrix}=\begin{bmatrix}5.25\0\-3.75\end{bmatrix}$
改正数:$v=QA^TK=\begin{bmatrix}1&&&&&\&1&&&&\&&1&&&\&&&1&&\&&&&1&\&&&&&1\end{bmatrix}\begin{bmatrix}0&1&0\0&1&-1\1&1&0\0&0&1\-1&0&0\-1&0&-1\end{bmatrix}\begin{bmatrix}5.25\0\-3.75\end{bmatrix}=\begin{bmatrix}0\3.75\5.25\-3.75\-5.25\-15\end{bmatrix}$
检验: \(\hat{h_3}=\hat{h_5}+\hat{h_6}\\ \hat{h_3}=-\hat{h_1}-\hat{h_2}\\ \hat{h_4}=\hat{h_2}+\hat{h-6}\)