lectures
chapter 3 条件平差
3.1 导入
数学问题:求函数$\frac{1}{2}v_1^2+v_2^2+\frac{1}{4}v_3^2$,满足:$\left{\begin{aligned}v_1+v_2+22=0\-v_2+v_3-10=0\end{aligned}\right.$的极值。根据高等数学安徽给你的拉格朗日乘常数法,组成新函数: $$ \begin{aligned} & \Phi=f+\lambda_1\varphi_1+\lambda_2\varphi_2=\frac{1}{2}v_1^2+v_2^2+\frac{1}{4}v_3^2-2k_a(v_1+v_2+22)-2k_b(-v_2+v_3-10)
\&
\begin{aligned}
&\frac{\partial\Phi}{\partial{v_1}}=v_1-2k_a=0
&\frac{\partial\Phi}{\partial{v_2}}=2v_2-2k_a+2k_b=0
&\frac{\partial\Phi}{\partial{v_3}}=\frac{1}{2}v_3-2k_b=0\
\end{aligned}
\rightarrow
\left {
\begin{aligned}
&v_1=2k_a
&v_2=k_a-k_b
&v_3=4k_b
\end{aligned}
\right .
\rightarrow
\left {
\begin{aligned}
&v_1+v_2+22=0
&-v_2+v_3-10=0
\end{aligned}
\right .
\rightarrow
\left {
\begin{aligned}
&3k_a-k_b+22=0
&-k_a+5k_b-10=0
\end{aligned}
\right .
\& \rightarrow
\left {
\begin{aligned}
&k_a=-7.143
&k_b=0.571
\end{aligned}
\right .
\rightarrow
\left {
\begin{aligned}
&v_1=-14.286
&v_2=-7.714
&v_3=2.284
\end{aligned}
\right .
\rightarrow
f_{min}=\frac{1}{2}v_1^2+v_2^2+\frac{1}{4}v_3^2=162.855 \end{aligned} $$
(1)数学上的求条件极值方法解决了条件模型解算
(2)概率论与数理统计理论助推提出最小二乘原理
(2)线性代数的向量和矩阵的运用
3.2 平差原理
(一)条件平差概念
条件平差:
未知数:观测值的平差值(或改正数)
未知数个数:观测数
未知数之间关系:存在条件
估值准则:$V^TPV=最小\rightarrow求条件极值$
间接平差:
未知数:参数,可以是直接观测量,也可以是间接观测值。
未知数个数:必要观测数
未知数之间关系:独立(任何一个参数都不能用其余的参数表示出来)
估值准则:$V^TPV=最小\rightarrow求自由极值$
例1:设有平面三角形,为确定三角形的形状,等精度观测了三个内角,其观测值分别是$L_1,L_2,L_3$以三个度数的最或然值$\hat{L_1},\hat{L_2},\hat{L_3}$为未知数,列出来未知数之间的条件关系式。
\[\hat{L_1}+\hat{L_2}+\hat{L_3}=180^\circ\]以$\hat{L_i}=\hat{L_i}+v_i(i=1,2,3)$代入上式,得 \(v_1+v_2+v_3+w=0\\ w=L_1+L_2+L_3-180^\circ\)
取全部观测量得改正数作为平差时得未知数,根据观测值得相互关系列出条件方程,根据最小二乘原理求满足条件方程得未知数得最或然值,并做出相应的精度评定,该过程为条件平差。
(二)基本数学模型
设 观测值为:$L_1,L_2,\cdots,L_n$;相应的改正数为:$v_1,v_2,\cdots,v_n$;观测值的平差值为:$\hat{L_1},\hat{L_2},\cdots,\hat{L_n}$,$\hat{L_i}=L_i+v_i(i=1,2,\cdots,n)$
向量表示 \(\hat{L}=\begin{bmatrix} \hat{L_1}\\\hat{L_2}\\\vdots\\\hat{L_n} \end{bmatrix} \qquad V=\begin{bmatrix} v_1\\v_2\\\vdots\\v_n \end{bmatrix} \qquad L=\begin{bmatrix} L_1\\L_2\\\vdots\\L_n \end{bmatrix} \qquad \hat{L}=L+V\)
共有$r=n-t$个条件方程 \(\hat{L}=L+V\\ A\hat{L}+A_0=0\\ AV-W=0\\ W=-(AL-A_0)\)
(三)条件平差的估值方程————改正数方程和联系数法方程
数学模型:
\[\mathop{A}\limits_{r{\times}n}\mathop{V}\limits_{r{\times}1}-\mathop{W}\limits_{r{\times}1}=0\\\mathop{D}\limits_{n,n}=\sigma^2_0\mathop{Q}\limits_{n,n}=\sigma^2_0\mathop{P^{-1}}\limits_{n,n}\\\]估值准则: \(V^TPV=min\)
设辅助函数 \(\Phi=V^TPV-2K^T(AV-W)\)
极值方程 \((\frac{d\Phi}{dV})^T=0\)
改正数方程 \(V=QA^TK\)
上式代入条件方程,得: \(AQA^TK-W=0\\ K=N^{-1}W\)
说明:
(1)法方程得阶数:N是rxr阶矩阵
(2)法方程得秩:rank(N)<=r
(3)当rank(A)=r时,称A行满秩,法矩阵N满秩,法方程有唯一解。
(四)条件平差公式总结
条件平差的数学模型为
\(\mathop{A}\limits_{r,n}\mathop{\Delta}\limits_{n,1}-\mathop{W}\limits_{r,1}=0 \tag{函数模型}\) \(\mathop{D}\limits_{n,n}=\sigma_0^2\mathop{Q}\limits_{n,n}=\sigma_0^2\mathop{P^{-1}}\limits_{n,n} \tag{随机模型}\) \(AV-W=0\\V^TPV=min \tag{平差模型}\)
\(AV-W=0 \tag{条件方程}\) \(AP^{-1}A^TK-W=0 \tag{法方程}\) \(NK-W=0 \qquad (AP^{-1}A^T=N)\)
\[K=N^{-1}W\] \[V=P^{-1}A^TK\\ \hat{\sigma_0^2}=\frac{V^TPV}{r}\](五)计算步骤
- 根据问题性质及观测量的情况,列出条件方程式。条件方程的个数等于多余观测数r。
- 由条件方程式组成联系数法方程,法方程的个数等于多余观测数。
- 解算法方程,求出联系数K。
- 将K代入改正数方程式,求出V值,并求观测值的最或然值$\hat{L}=L+V$。
- 为了检验平差计算的正确性,常常要将各最或然值$\hat{L_i}$代入原条件方程式,看其是否闭合。
- 精度估计。


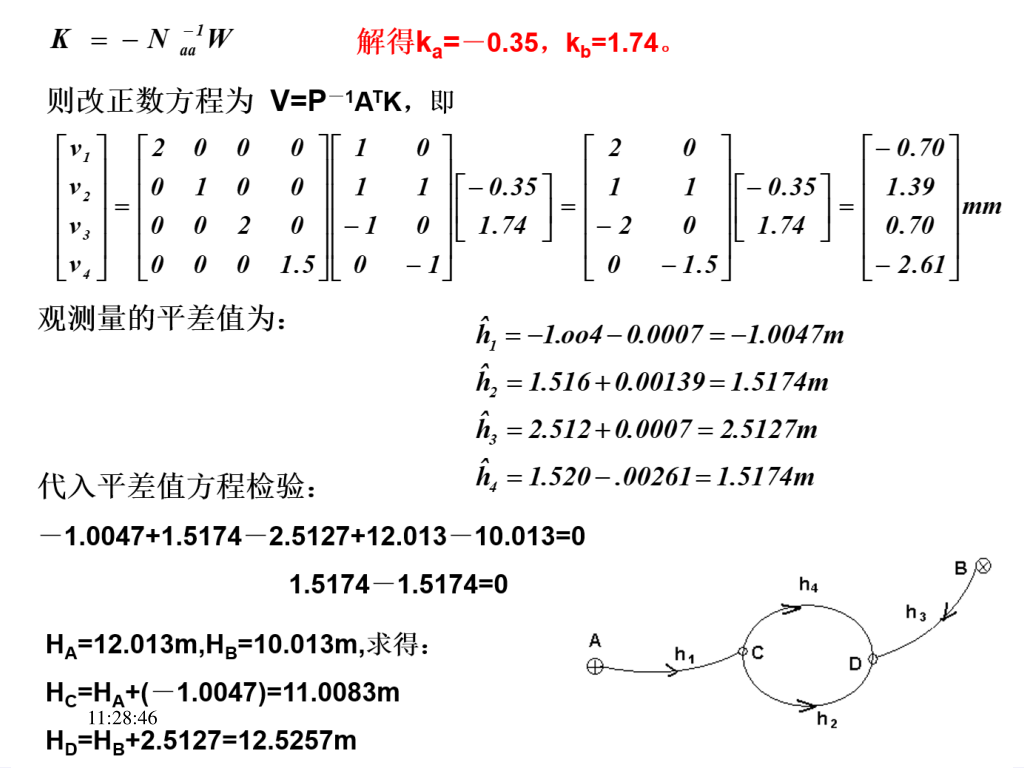
3.3 条件方程
3.4 精度估计
通过观测值的改正数V来计算单位权方差和中误差: \(\hat{\sigma_0^2}=\frac{V^TPV}{r}\)
平差值函数的方差 \(D_{FF}=\hat{\sigma_0^2}Q_{FF}\)
谐因数传播律 \(Z=KX+K_0\\ Q_{ZZ}=KQ_{XX}K^T\)
3.5 公式汇编及举例
条件平差的函数模型和随机模型是 \(AV+W=0\\ D=\sigma_0^2Q=\sigma_0^2P^{-1}\)
条件方程: \(AV+W=0\)
法方程: \(N_{aa}K+W=0\)
改正数方程: \(V=P^{-1}A^TK=QA^TK\)
观测量平差值: \(\hat{L}=L+V\)
平差值函数: \(\hat{\varphi}=f(\hat{L_1},\hat{L_2},\cdots,\hat{L_n})\)
权函数式为: \(d\hat{\varphi}=f_1d\hat{L_1}+f_2d\hat{L_2}+\cdots+f_nd\hat{L_n},(f_i=\frac{\partial f}{\partial \hat{L_i}})_{L_i}\)
单位权方差的估值: \(\hat{\sigma_0^2}=\frac{V^TPV}{r},\hat{\sigma_0}=\sqrt{\frac{V^TPV}{r}}\)
平差值函数的方差: \(\hat{\sigma^2_{\hat{\varphi}}}=\sigma_0^2Q_{\hat{\varphi}\hat{\varphi}}=\sigma_0^2[f^TQf-(AQf)^TN^{-1}_{aa}AQf]\)